Probability and Odds

As you probably know, most real-world events cannot be predicted with total certainty. Probability and odds describe how likely an event is to happen. In this module we will discuss how probability and odds are used to predict everyday situations. We are also going to explain how probability and odds are integral to the understanding of important biological concepts, such as Punnett squares and the Hardy-Weinberg equation.

Probability

Probability measures the likelihood that an experiment will end in a specific result. When calculating probability, we often consider the number of ways that our result can occur, along with the total number of possible outcomes to our experiment. The most common way to assign probabilities is using a uniform probability model. The general equation for uniform probability is:

$P (x) = \frac{number of possible outcomes that match our result}{total number of possible outcomes}$

Where $x$ is the result of interest.

In the next two examples, consider rolling a standard, six-sided die once.

Example 1. What is the probability of rolling a 2?

You can probably figure this one out quickly in your head. There are six possible outcomes when rolling a die, with one number (1-6) on each side.

In this situation, the only outcome that satisfies your result (rolling a 2), is, in fact, rolling a 2. Being a six-sided die, the total number of possible outcomes is 6, since you could roll a 1, 2, 3, 4, 5, or 6.

Using the uniform probability equation given above:

$P (2) = \frac{(number of possible outcomes that satisfy the result)}{(number of total possible outcomes)} = \frac{1}{6}$

So the probability of rolling a 2 is $\frac{1}{6}$ .

Example 2. What is the probability of rolling an even number?

Because numbers on a die are 1-6, rolling an even number would require rolling a 2, a 4, or a 6. Any of these three outcomes would satisfy the result.

$P (2, 4, or 6) = \frac{3}{6} = \frac{1}{2}$

So the probability of rolling an even number is $\frac{1}{2}$ .

Probability is always given on a scale from 0 to 1. Having a probability of 0 usually means that it is impossible for the event to happen. Having a probability of 1 means that the event is certain to happen. Because probability is given between 0 and 1, it is often expressed as a fraction, as seen in the previous examples. However, another way to express probability is as a percentage. The probability in Example 2 was $\frac{1}{2}$ .

This means that you would expect the die roll to result in an even number about half of the time, or 50% of the time.

Now we will do a few more examples involving basic probability. Instead of dice, we will now work with marbles. Let's say you have a bag of marbles that contains 4 green marbles, 5 yellow marbles, 2 red marbles, and 1 blue marble.

Example 3. When drawing one marble from the bag, what is the probability that the marble you draw is yellow or blue?

$P (blue or yellow) =$ $\frac{1 blue + 5 yellow}{12 total marbles}$

$P (blue or yellow) = \frac{6}{12}$

$P (blue or yellow) = 50 %$

Sometimes you may want to know the probability of two events occurring at the same time. For instance, what is the probability of drawing a yellow marble, putting it back in the bag, and then drawing another marble and it being red? In order to do this, we need to use the product law.

Product Law

When experiments occur sequentially, the combined probability of the results is equal to the product of their individual probabilities.^[1] For example, if you have two experiments you can calculate the probability of two sequential results by taking the probability of the first result and multiplying it by the probability of the second result. Let’s look at a situation with marbles again, this time with two marbles being drawn sequentially.

Example 4. What is the probability of drawing a yellow marble and then, after putting it back in the bag, drawing another marble and it being red?

First, we need the probability of drawing a yellow marble: $\frac{5}{12}$

Next, we need the probability of drawing a red marble (keep in mind that there are still 12 marbles to choose from): $\frac{2}{12}$

Now, to see what the probability of this scenario occurring, we find the product of the two probabilities:

$P (yellow then red) = \frac{5}{12} \times \frac{2}{12}$

$P (yellow then red) = \frac{10}{144}$

$P (yellow then red) = \frac{5}{72}$ , or $6.9 %$

So there is a 6.9% chance that you will draw a yellow marble followed by a red one.

Odds

Another way to express the likelihood of a result is by using odds. The odds of a result is the probability of an event to it’s complement. It is written in ratio form. When finding odds, we still use the number of outcomes that satisfy the result, but instead of using the total number of possible outcomes, we use the number of outcomes that do not satisfy the result.

Odds are usually expressed in one of these ratio forms:

Odds in Favor:

Number of possible outcomes that satisfy the result :

Number of possible outcomes that do not satisfy the result

Odds Against:

Number of possible outcomes that do not satisfy the result :

Number of possible outcomes that satisfy the result

Example 6. Say you are rolling a standard, six-sided die once. What are the odds of rolling a 2?

We know that rolling a 2 is the only outcome that satisfies this result. This means that the other five outcomes do not satisfy the result.

By using the ratios given above, we can say that the odds in favor of rolling a 2 are 1:5.

The odds against rolling a 2 are just the opposite: 5:1.

Example 7. Recall from earlier that you hae a bag of marbles with 4 green, 5 yellow, 2 red, and 1 blue. What are the odds of drawing a yellow or blue marble?

Since there are 5 yellow marbles and 1 blue marble in the bag, we have 6 outcomes that satisfy the result. This means that the other 6 outcomes do not satisfy the result.

So in this case, the odds in favor and the odds against are equal, as they are 6:6.

The odds of 6:6 can be reduced to 1:1 and can also be called even odds.

Life Science Applications

Now that you know the basic information about probabilities and odds, we are going to go through a few examples of their applications in biology.

Mendelian Genetics and Punnett Squares^[2]

As you may have already learned, Mendel and his pea plants gave us priceless knowledge about the foundations of genetics and inheritance. We can use what we have learned about probability to calculate the chance of obtaining certain traits or combinations of traits from classic Mendelian crosses.

Example 8. Let’s look at two independently assorted traits in pea plants: seed color and plant height. We’ll denote seed color as G (yellow) and g (green), and plant height by D (tall) and d (dwarf).

Seed Color

Let’s first consider a simple cross where each parent has yellow seeds – one is homozygous (GG) and one is heterozygous (Gg).

Parents: Gg x GG

As you can see from the Punnett square above, the genotypic ratio of the first filial generation F₁ is 2:2 (GG:Gg) because there are two GG and two Gg possibilities.

Because all the possible genotypes produce yellow seeds, the phenotypic ratio is 4:0 (yellow:green).

Plant Height

Now we’ll look at the height of the plants. This time each parent is heterozygous (Dd).

Parents: Dd x Dd

Here the genotypic ratio of the F₁ is 1:2:1 (DD,Dd,dd). In this example we have more than one phenotype produced, with a phenotypic ratio of 3:1 (tall:dwarf).

Now that we know the probabilities of each of the random fertilization events, what is the probability of an F₁ offspring having the genotype GG or dd?

We could set up a dihybrid cross, but we are going to take the easier route by multiplying the probabilities from the ratios above.

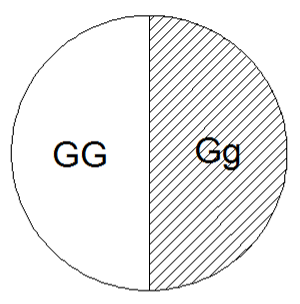
Let’s think about this two ways: graphically and numerically.

This pie charge represents the probability of obtaining each genotype in the F₁ generation from the parent cross GG x gg. Since both probabilities are equal they must each be $\frac{1}{2}$ .

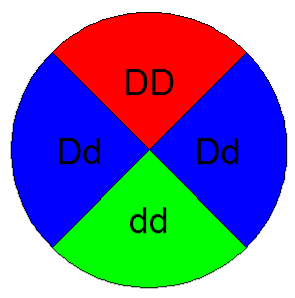
This pie chart represents the probability of obtaining each genotype in the F₁ generation from the parent cross DD x dd. The probabilities for DD and dd are each $\frac{1}{4}$ and the probability of Dd is $\frac{1}{2}$ .

Now to find the probabilities for all combinations of genotypes for our two traits, we merge the pie charts.

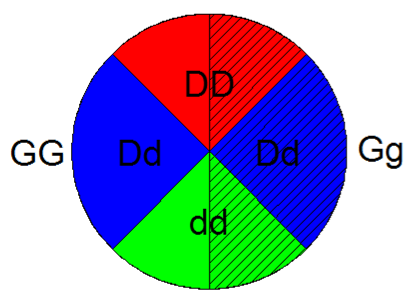
Let's consider one half of the chart, for example the GG side: $\frac{1}{4}$ of this half will also be DD, $\frac{1}{2}$ of this half will be Dd , and $\frac{1}{4}$ of this half will be dd. The same is true for the Gg half.

Recall that we are looking for the probability that an F₁ individual would inherit either the GG or dd genotype. We can look at the pie chart above to calculate the probability. First, we need all the “slices” of the pie containing GG, so that means the 4 slices on the left side are counted. Next, we want look specifically for the dd slices on the chart. We can see that there are 2 dd slices, but one of them has already been counted as a GG slice, so we can disregard it. The single dd slice from the gg side of the chart is $\frac{1}{8}$ of the total. We add this slice to $\frac{4}{8}$ (the entire GG half) to get a probability of: $\frac{1}{8} + \frac{4}{8} = \frac{5}{8}$

Now let’s try looking at this with numbers and equations instead of pie charts.
Refer to the genotypic ratios we calculated using Punnett squares.

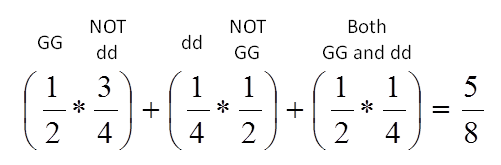
Hardy-Weinberg Equilibrium Equation^[3]

Evolution is a change in the allele frequencies in the gene pool of a population over time. To demonstrate this, assume there is a trait that is determined by the inheritance of a gene with two alleles: A and a. In the parent generation, there is 92% A and 8% a. When the F₁ generation results, there is a change in allele frequency to 90% A and 10% a. Evolution has occurred in the population.

This definition of evolution was developed largely in response to the work of Godfrey Hardy and Wilhelm Weinberg. In the early 1900s, they created a mathematical model based on probability to discover probable genotype frequencies in a population and track them from generation to generation.

In order to understand Hardy's and Weinberg's model, let's think about a population of 100 individuals. Forty (40) of these folks are homozygous dominant (genotype AA), 50 of them are heterozygous (genotype Aa), and the other 10 are homozygous recessive (genotype aa). These are the frequencies of the genotypes, but what are the frequencies of the alleles?

Each of the 40 AA individuals have two A alleles, which gives us a total of 80 A alleles. By the same token, the 50 Aa individuals each have 1 A allele. So the total number of A alleles in our population is (2×40)+50=130(2×40)+50=130. Similarly, there are (2×10)+50=70(2×10)+50=70 a alleles in this population.

From these counts we can find allele frequencies, which are the proportions of A and a alleles in this population. We will call the A proportion p and the a proportion q. Note that each individual has two alleles, so we actually have twice as many alleles as individuals in the population.

$p = \frac{(2 \times 40) + 50}{2 \times 100} = \frac{130}{200} = 0.65$

$q = \frac{(2 \times 10) + 50}{2 \times 100} = \frac{70}{200} = 0.35$

In general, if we have a population of N individuals with n_AA of them being homozygous dominant, n_nAa heterozygous, and n_aa homozygous recessive, then:

$p = \frac{(2 \times n_{A A}) + n_{A a}}{2 \times N}$

$q = \frac{(2 \times n_{a a}) + n_{A a}}{2 \times N}$

Since we are dealing with two alleles, the frequency of one plus the other must be 100%, or p + q = 1.

For a population to continue, there needs to be mating that produces offspring. Absent any information as to how partners are chosen, we will use randomness as a model. If we assume that females and males in our population both have the same allele frequencies p and q, then, for example, the proportion of homozygous dominant offspring in the F₁ will be about p x p. To illustrate we can look at the Punnett square for the population:

Now we can see from the Punnett square that:

p² + 2pq + q² = 1

The frequencies of all four gametes have to add up to 1, or100%.
This simple equation is known as the Hardy-Weinberg equilibrium equation.

Now let's think about the type of information we usually have about a population. Since genotypes are difficult to collect on an entire population, we usually gather data on phenotypes instead. The genotypes expressing the dominant trait are either AA or Aa. Hardy-Weinberg tells us that p² + 2pq of our population will be phenotypes expressing the dominant trait.

Looking at the recessive individuals, we know that they are all genotype aa and Hardy-Weinberg tells us that there should be q² of them. If we know the frequency of recessive individuals, we know q² and we can then calculate q.

Using the relationship p + q = 1, we can see that p must equal 1−q. Therefore, if we know q, we can find p!

Now that we have values for p and q, we can “plug and chug” into the Hardy-Weinberg equation to get the predicted frequencies of all three genotypes.

As we have already seen, Punnett squares and the Hardy-Weinberg equation are closely related. Punnett squares allow us to predict probabilities of offspring genotypes based on known parental genotypes. The Hardy-Weinberg equation allows us to do this for entire populations.

Let’s do a problem using the Hardy-Weinberg equation.

Example 9. Albinism is a genetically inherited trait that is expressed by homozygous recessive individuals (aa). The average human frequency of albinism in North America is only about 1 in 20,000. What are the predicted frequencies of each of the three genotypes (AA, Aa, aa)?

Looking back at the Hardy-Weinberg equation ( $p^{2} + p q + q^{2} = 1$ ), we see that $q^{2}$ stands for homozygous recessive frequency (aa) and we know the frequency of aa is 1 in 20,000 individuals. We can expres this as:

$q^{2} = \frac{1}{20, 000}$
$q^{2} = 0.00005$
Take the square root of both sides to find q:

$\sqrt{q^{2}} = \sqrt{0.00005}$
After rounding, we see that:

$q = 0.0071$
This tells us that the frequency of the recessive albinism allele (a) is 0.0071 or about 1 in 140. Now that we know q, let's solve for p:

$p = 1 - q$
$p = 1 - 0.0071$
$p = 0.9929$
Now we know that the frequencyof the dominant allele (A) is 0.9929, or about 99 in 100. Next, we need to put the known values for p and q into the Hardy-Weinberg equation to give us the frequencies of each of the three genotypes in the population:

$p^{2} + 2 p q + q^{2} = 1$
$(0.9929)^{2} + [2 (0.9929) (0.0071)] + (0.0071)^{2} = 1$
By rounding, the equation is now:

$0.9859 + 0.0141 + 0.0005 = 1$
By breaking these values down, we see that:

$p^{2} = predicted frequency of homozygous dominant = 0.9859 = 98.59 %$

$2 p q = predicted frequency of heterozygous = 0.0141 = 1.410 %$

$q^{2} = predicted frequency of homozygous recessive = 0.00005 = 0.005 %$

As we can see, albinism is rare, but with a frequency of 1.4%, heterozygous carriers (Aa) are more common that we might expect.

Sensitivity and Specificity^[4]

Let’s say a new screening test for cancer has been developed and our lab has assembled two groups on which the test will be piloted. One group comprises individuals known to have the cancer and the other comprises individuals known to be free of the cancer. Our goal is two-fold: 1) to determine the probability of the test giving a positive result when it is actually positive – sensitivity, and 2) to determine the probability of the test giving a negative result when it is actually negative – specificity. Ideally, both of these values will be as close to 1 as possible. That is, the test will be accurate both for people with the cancer and people without it.

We are now going to do an example involving cervical cancer and the screening test called a Pap smear.

Example 10. Cervical cancer is a disease that can be detected early. The Pap smear is the main type of screening procedure used to detect this cancer before it produces symptoms. In 1972, 1973, and 1978, a research team assessed the competency of technicians who scan Pap smear slides for abnormalities.

Overall, 16.25% of the tests performed on individuals with cervical cancer resulted in false negative outcomes. A false negative occurs when a disease is present in an individual but the test result is negative (saying that the individual does not have the disease).

Therefore, in this study:

$P (test negative | cancer) = 0.1625$
(the vertical bar means "given")

The other 100 - 16.25 = 83.75% of the individuals who had cervical cancer did, in fact, test positive. As a result:

$P (test positive | cancer) = 0.8375$

The probability of obtaining a positive test result when the individual being tested actually has the disease is called the sensitivity of the test. in this test, the Pap smear had a sensitivity of 0.8375.

Not every individual tested actually had cervical cancer. Of those who did not have cervical cancer, 18.64% of them tested positive. A false positive occurs when there is no disease present in an individual who tests positive. This tells us that:

$P (test positive | no cancer) = 0.1864$

The specificity of a test is the probability that the test result is negative when the individual being tested does not have the disease. In this study, the Pap smear had a specificity of:

$P (test negative | no cancer) = 1 - 0.1864$

$P (test negative | no cancer) = 0.8136$

To recap, the sensitivity is found by the equation: sensitivity = 1 - (false negative)

and specificity is found by the equation: specificity = 1 - (false positive)

Testing Model Fit

Science often involves proposing (and subsequently testing) models. Thus, the ability to evaluate models empirically (i.e. using data) is an essential skill.

As we explored in Cell Biology, specific ratios are expected to emerge from certain mating crosses. The ratio 9:3:3:1, for example, is expected for a heterozygous dihybrid cross. When we assume data will fit a given ratio, we have established a model for the process that generated the data. If the model is viable (Careful! We can’t really prove if a model is “correct”), then the data should agree with the model’s predictions. If the data do not agree with the predictions, then the model is probably not a good one.

One of the simplest statistical tests devised to test models is the chi-square (χ2) analysis. This test takes into account the observed “deviation” (prediction error) for each prediction and aggregates them to a single numerical value.

The formula for chi-square analysis is:

$χ^{2} = \sum \frac{(o - e)^{2}}{e}$

Where o is the observed value for a given prediction, e is the expected (predicted) value, and ∑ represents the sum of the calculated values for each ratio. Because $(o - e)$ is the deviation $(d)$ , the equation can be reduced to:

$χ^{2} = \sum \frac{d^{2}}{e}$

A common example for this type of model evaluation comes from testing Mendel's theory of natural inheritance. In one experiment, Mendel crossed all-yellow pea plants with all-green pea plants. He predicted that the F₁ generation would contain 75% yellow seeds and 25% green seeds. The experiment ended up producing n=8023 seeds.

Following Mendel’s theory, we would expect the following numbers of yellow and green seeds:

0.75 * 8023 = 6017.25 seeds should have been yellow and

0.25 * 8023 = 20005.75 seeds should have been green.

These are the expected values.

In fact, of the 8023 seeds produced in this experiment, 6022 were yellow and 2001 were green. These are the observed values.

Does this mean Mendel’s theory is wrong? How close are the actual data to the predicted results of Mendel’s theory?

To answer this question, we can use chi-square analysis.

To calculate the $χ^{2}$ statistic, we enter our expected and observed values in to the equation:

$χ^{2} = \sum \frac{(o - e)^{2}}{e} = \frac{(6022 - 6017.25)^{2}}{6017.25} + \frac{(2001 - 2005.75)^{2}}{2005.75} = 0.015$

If our model is perfect then all of the (o−e)s will be 0, which means the χ2 statistic will be 0. If our model is “good” then all of the (o−e)s should be “small” which means that the χ2 statistic will be “small.” If our model is “bad” then at least one of the (o−e)s will be “large” so our χ2 statistic will be “large.”

How do we distinguish between large χ2 values and small ones? The result 0.015 seems small, but is it?

Just like we have a model for our data, we also have a model for our χ2 statistic. Most of the time, if our model is good, we should get a small χ2 value. Sometimes we get a large χ2 value, but just due to random variation. If our model is correct, how often can we expect to get a χ2 statistic as large as 0.015 (or larger)?

The model we use to evaluate our χ2 statistic is called (appropriately enough) a χ2 model. A χ2 model may look like this, for example:

This figure shows smaller values are more common and larger values are more rare.

A $χ^{2}$ model contains a parameter called degrees of freedom that governs the difference between "small" and "large" $χ^{2}$ values.

The larger the degrees of freedom, the larger the value that distinguishes between “small” (good model) and “large” (bad model). In this case, the degrees of freedom will be the number of categories (i.e. predictions) minus one. This makes sense since the more predictions we make, the more terms we add to the $χ^{2}$ statistic, which just makes the $χ^{2}$ statistic larger regardless of how good our model is. Since Mendel made two predictions (75% yellow and 25% green), the degrees of freedom for this example will be 2-1 = 1.

We can use software like Excel to calculate a p-value for our $χ^{2}$ statistic. In this case, the p-value is the probability of obtaining a $χ^{2}$ statistic of 0.015 or higher if our model is good. In Excel we can select an empty cell and type = CHIDIST(0.015,1), which returns a value of 0.9025. this means that a good model will generate data that has a $χ^{2}$ statistic of 0.015 or greater about 90.25% of the time. Therefore, these data do not contradict Mendel's theory. If the p-value would have been small, say .05 (5%) or less, then we could conclude that the data did not fit Mendel's model, which would have indicated Mendel's model was bad (which is not the case).

References

Citations

Klug et. al. (2009), p. 43
Klug et. al. (2009), p. 41
D. O'Neil, (2011)
Klug et. al. (2009), p. 136

Bibliography

O’Neil D (2011). “Hardy-Weinberg Equilibrium Model.” http://anthro.palomar.edu/synthetic/synth_2.htm.

Klug WS, Cummings MR, Spencer CA and Palladino MA (2009). Essentials of Genetics, 7 edition. Benjamin Cummings. ISBN 0321618696.

Glossary

Monohybrid Cross: A genetic cross between two true-breeding individuals from different parental strains that differ in a single trait, such as seed color (e.g., yellow vs. green). The purpose is to observe the inheritance pattern of this trait in offspring.

Parental Generation (P₁): The initial set of individuals used in a genetic cross, which are true-breeding for specific traits.

First Filial Generation (F₁): The first generation of offspring produced from the cross of the parental (P₁) generation.

Second Filial Generation (F₂): The second generation of offspring, produced by self-fertilizing the F₁ individuals, or by crossing F₁ individuals with each other.

Phenotype: The observable characteristics or traits of an organism, resulting from the interaction of its genotype and environmental influences (e.g. yellow seeds or green seeds in plants).

Genotype: The genetic constitution of an individual organism, referring to the specific alleles it carries for a particular trait (e.g. "AA", "Aa", or "aa" for seed color).

Genes: Segments of DNA that carry the instructions for producing RNA and/or protein, and are the basic units of heredity that determine traits.

Alleles: Different versions of a gene that arise by mutation and are found at the same location on a chromosome. Alleles can be dominant or recessive, influencing the expression of a trait (e.g. tall allele and dwarf allele for plant height).

Homozygous: An organism with two identical alleles for a particular gene (e.g. "AA" or "aa").

Heterozygous: An organism with two different alleles for a particular gene (e.g. "Aa").

Punnett Square: A graphical tool used to predict the genotype and phenotype ratios of offspring resulting from a particular genetic cross. It illustrates all possible combinations of alleles from the parents.

Independent Assortment: The principle that alleles for different traits segregate, or assort, independently of one another during the formation of gametes. This occurs during meiosis, leading to genetic variation. An exception to the law of independent assortment is for genes that are located very close to one another on the same chromosome.

Product Law of Probabilities: A statistical principle used to calculate the probability of multiple independent genetic events occurring simultaneously. It states that the probability of two or more independent events occurring together is the product of their individual probabilities.

Probability and Odds

Probability and Odds

Probability

Product Law

Odds

Life Science Applications

Mendelian Genetics and Punnett Squares[2]

Seed Color

Plant Height

Now that we know the probabilities of each of the random fertilization events, what is the probability of an F1 offspring having the genotype GG or dd?

Testing Model Fit

References

Citations

Bibliography

Glossary

Mendelian Genetics and Punnett Squares^[2]

Now that we know the probabilities of each of the random fertilization events, what is the probability of an F₁ offspring having the genotype GG or dd?