Fitting Lines

Linear Regression is a technique based on fitting a straight line to data. This includes analyzing the relationship between two quantitative variables, usually x and y^[1].

Linear regression is intricately linked to the concepts of correlation, slope, intercept, and various descriptive coefficients. In this module, we will learn about the basics of linear regression and discuss why a linear relationship is useful.

Slope

We will start by going over the basics of slope. For a linear function, the average rate of change is called the slope of the line^[2].

The slope of a line through points with coordinates (x1,y1) and (x2,y2), when x1 does not equal x2, can be found using this formula:

(y2-y1)/(x2-x1).

We usually learn this formula as “rise over run”, where rise is the difference between the y-axis points and run is the difference between the x-axis points.

NOTE: If x2=x1, then the points are on a vertical line and the slope is undefined. This applies to all vertical lines.

Example

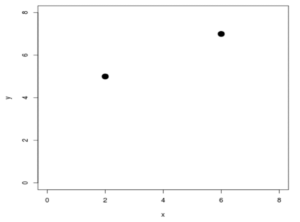
Find the slope of the line that contains the points (2,5) and (6,7), shown in Fig. 1.

Let’s first define our points:

x1 = 2

y1 = 5

x2 = 6

y2 = 7

Solution

Using the formula (y2-y1)/(x2-x1), we next plug in the values for x1, y1, x2, and y2 to solve for slope:

slope=(7-5)/(6-2)

slope=2/4

slope=1/2

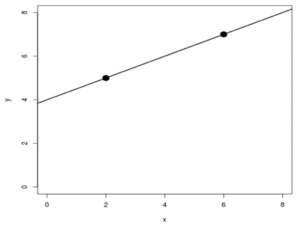
Looking at Fig. 2, we can see that for every two-unit increase on the x-axis (run), there is a one-unit increase on the y-axis (rise).

Intercept

The graph of y=mx+b is a line with slope m that goes through the point (0,b)^[3].

b is called the y-intercept because it is the point on the y-axis where the value is 0.

Example

Write the equation 2x-3y=6 in slope intercept form and identify the y-intercept.

Solution

First, isolate the y term:

-3y=-2x+6

Then solve for y:

y=(2/3)x-2

The slope m = 2/3 and the y-intercept b = -2.

Fitting Lines to Data

Fitting lines to data can help us determine the relationship between two variables. To do this, we first graph our data points and then draw a straight line that gets as close to as many data points as possible. We can do this by hand, and then use software applications to create a more accurate line through the data points.

Example

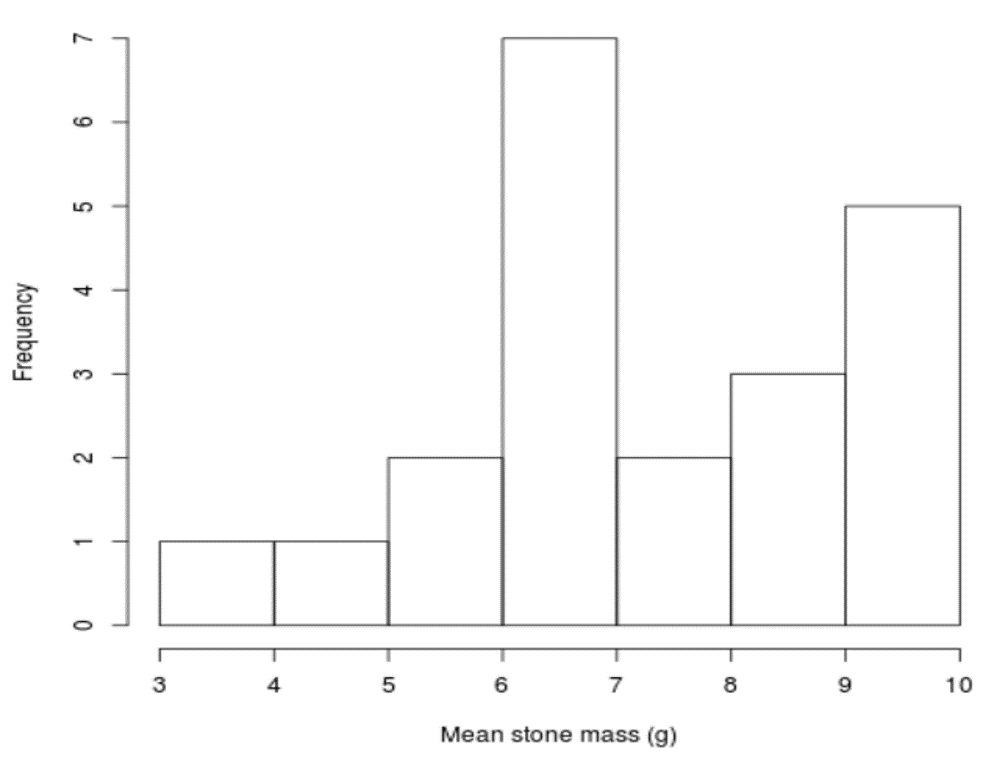
Soler et al. recorded the average stone mass (in grams) carried by 21 male black wheatears^[4]. The researchers observed that some male black wheatears tended to carry heavier stones than others (Fig. 3). Female black wheatears may see these stronger males as better mates. That is, the females use the stone size (which is easy to observe) as a proxy for the health of the males (which is more difficult to observe).

Black wheatears are small black birds from the western Mediterranean region. Male black wheatears engage in a mating ritual where they carry heavy stones (relative to their body weight) to nesting sites in caves in order to impress females.

This is all well and good, but is there evidence of a link between average stone mass and the health of male black wheatears?

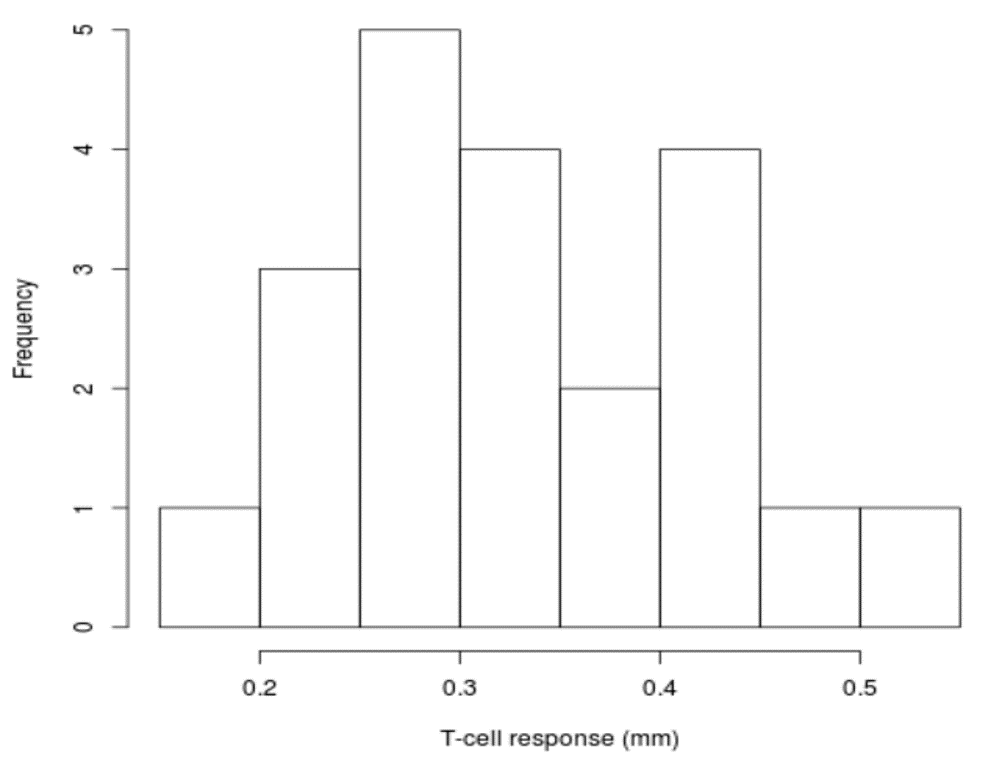
To look at this question, Soler et al. measured immune system response in the 21 male black wheatears by measuring T-lymphocyte response to a wing injection of a compound called phytohemagglutinin (PHA). The immune response could be measured (in mm) by a web that formed on the wing.

The data are shown in Fig. 4 and indicate that some male black wheatears mounted a higher immune response than others to the PHA injection.

Do the male black wheatears who had a stronger immune response also carry heavier stones?

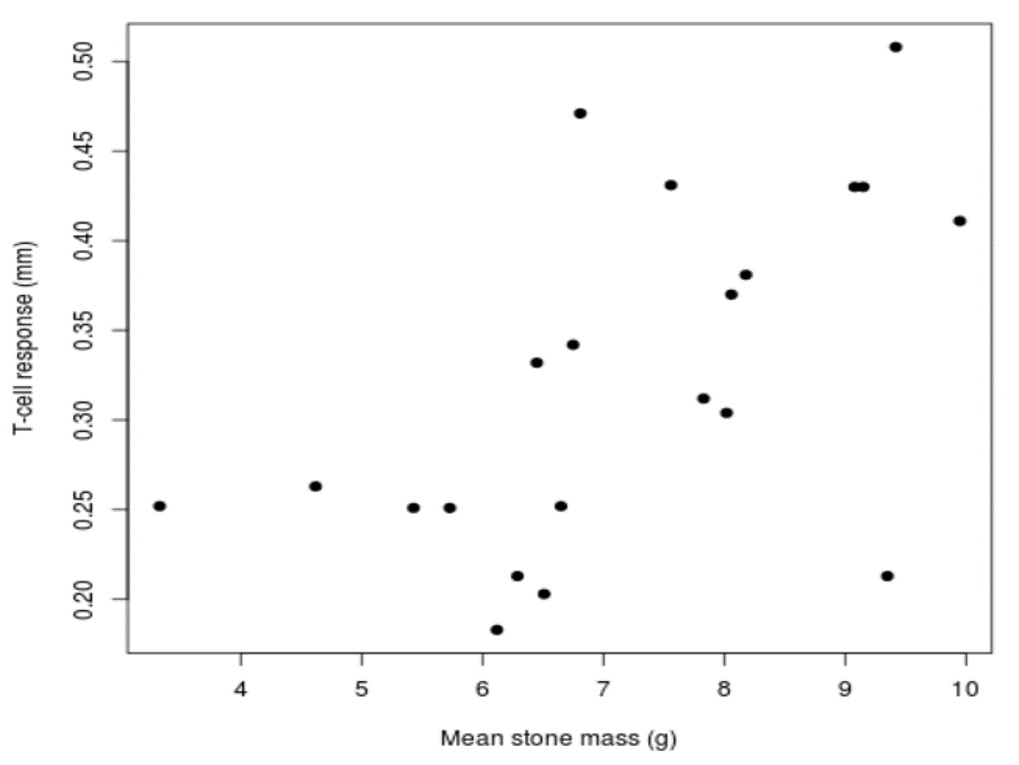
We can find out if there is a relationship between immune response and stone mass by creating a scatterplot of T-cell response vs. mean stone mass (Fig. 5).

Each of the 21 male black wheatears is represented by a single dot on the scatterplot. The horizontal position of each dot represents mean stone mass carried by that individual, and the vertical position represents that individual’s T-cell response.

It appears that males who carried heavier stones tended to have a stronger immune response than males who carried lighter stones. Note that this is only a tendency. Not every male in the sample followed this pattern. But from simply looking at the scatterplot we can conclude that if a female is interested in finding a healthy mate, she should look for males who carry heavier stones.

To better communicate and summarize the relationship between immune response and mean stone mass carried, we need to fit a line to the scatterplot data (Fig. 6).

Lines fit to data are often called lines of best fit or regression lines. Most data analysis software can fit these lines.

The blue line of best fit shown in Fig. 6 is given by the equation: y=0.03283x+0.08750

It can be more informative to replace y and x with the names of the variables they represent:

T-cell response ≈ 0.03283(mean stone mass) + 0.08750

NOTE: We replace the equals sign with an approximately equals sign to reflect the fact that not every data point lies on the best fit line.

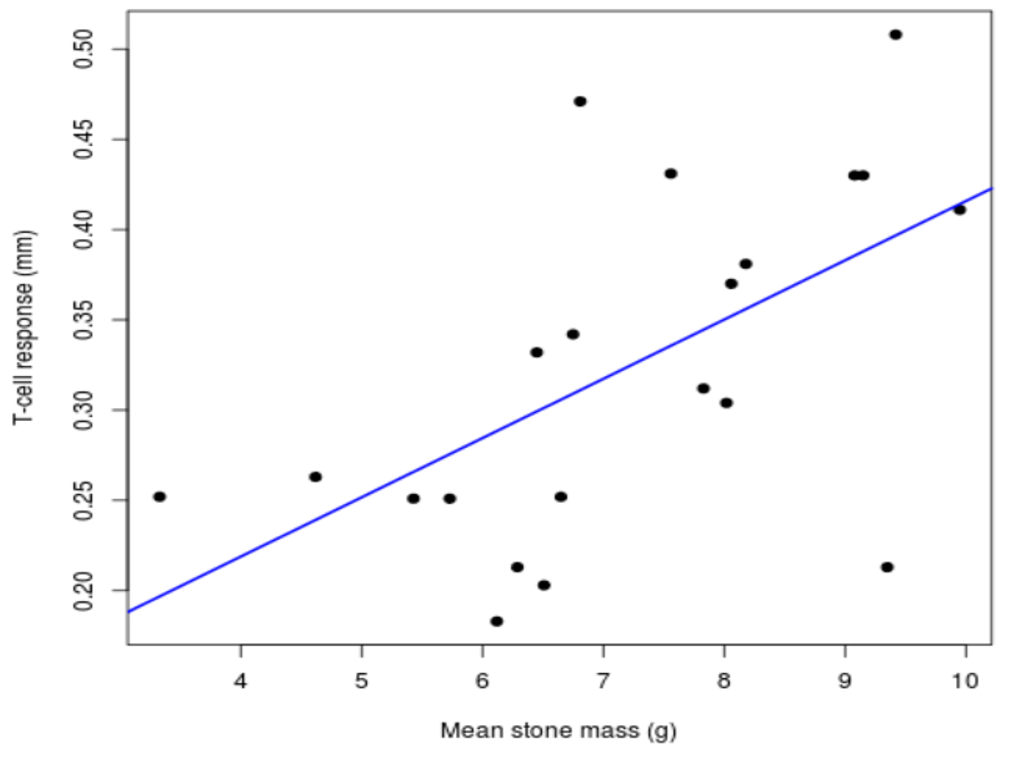
Now we can interpret the slope and intercept:

Slope: For every one-gram increase in mean stone mass, we can expect about a 0.03282 mm increase in T-cell response.
Intercept: For a male black wheatear carrying an average stone mass of zero grams, we expect a wing web T-cell response of about 0.0875 mm.

NOTE: It is always dangerous to make projections outside the range of our data. Since we did not actually measure any male black wheatears with a mean stone carrying mass of zero grams, we should not put too much stock in the interpretation of our intercept. The interpretation was given just for example purposes.

Coefficient of Determination

A statistic often used in the context of regression lines is the coefficient of determination, also known as R², which measures the proportion of variation in the response variable (y) that can be explained by the change in the (x) variable.

Another way to think about R² is to ask the question; “On a scale from 0 to 1 (0% to 100%), how well does our regression line describe the relationship between the x and y variables?”

If R² = 0, then the regression line does not describe the relationship between the x and y variables at all. On the other hand, if R² = 1, then the regression line describes the relationship between the x and y variables perfectly. R² gives us the percentage of the data points that will fall on the line of best fit.

In our male black wheateater example, R²= 0.3336. This means that 33.36% of the variation in T-cell response can be modeled using the mean stone mass carried by the bird. Therefore, female black wheatears can use mean stone mass carried as a proxy for immune health, it just won’t be a highly accurate predictor of immune strength.

Correlation Coefficient

You might be wondering what R represents. R is the the correlation coefficient, and Pearson’s correlation is the most common type of correlation coefficient.

R can be a value between -1 and 1, and it also describes the relationship between the x and y variables. When R is positive, the y values increase as the x values increase. When R is negative, the y values decrease as the x values increase.

Something to keep in mind is that the Pearson’s correlation only indicates whether there is a linear relationship between the x and y variables. It does not tell us whether y is dependent on x or whether x is dependent on y. In other words, it does not know whether x or y is the dependent or independent variable.

References

1. Samuels ML, Witmer JA and Schaffner A (2011). Statistics for the Life Sciences, 4 edition. Addison Wesley. p. 480. ISBN 0321652800..

2. Dugopolski M (2002). Precalculus Functions and Graphs and Precalculus with Limits Functions and Graphs, 1st Edition; Instructor’s Edition edition. Pearson Education, Inc.; Addison Wesley. p. 160. ISBN 0201734613.

3. Dugopolski M (2002). Precalculus Functions and Graphs and Precalculus with Limits Functions and Graphs, 1st Edition; Instructor’s Edition edition. Pearson Education, Inc.; Addison Wesley. p. 160. ISBN 0201734613.

4. Soler M, Martín-Vivaldi M, Marín JM, Møller AP (1999). “Weight lifting and health status in the black wheatear.” Behavioral Ecology, 10(3), pp. 281 –286. https://academic.oup.com/beheco/article/10/3/281/201579.

5. Ramsey F and Schafer D (2002). The Statistical Sleuth: A Course in Methods of Data Analysis, 2 edition. Duxbury Press. p. 221. ISBN 0534386709.